Sudoku Finds
Some time ago I solved sudoku and made the following observation.
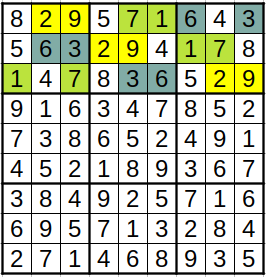
In the sudoku above in the first row of 3 blocks of 3x3 cells
you see the following pattern emerge.
(2,9) + 4 or 5 or 8
(1,7) + 4 or 5 or 8
(3,6) + 4 or 5 or 8
This pattern is always the case,
however with one exception, which I show shortly.
And this pattern goes for all rows of blocks of 3x3 cells,
and also for all columns of blocks of 3x3 cells.
To show you that this pattern is not just an incident, consider
Instead of the digits 1,2,...9 we use the letters A, B, … I
The general rule for sudokus is
Each row, column and 3x3 block must contain the digits 1 through 9
exactly once.
We can split this into 2 rules.
For each row of 3x3 blocks, each letter must be in one row and one
block.
For each column of 3x3 blocks, each letter must be in one column and
one block.
Now let us consider one row of blocks of 3x3 cells.
We randomly place the letters while adhering to the rule for a row of
bocks.
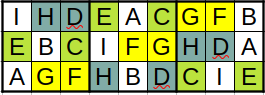
You can see the pattern emerge.
(H,D) + A or B or I
(C,E) + A or B or I
(G,F) + A or B or I
Of course you can also do this with a column of blocks.
Now the promised second pattern sets of 3.
Notice that in sets the sequence of the elements do not matter.
We can put these in a row of blocks while sticking to the rules, see
below.
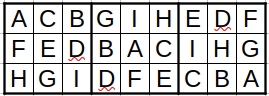
Can you see the sets of 3 (A,B,C), (D,E,F) and (G,H,I)?
Now to conclude my finds, one very special case with only sets of 3.
Also notice that the sets are actually tuples,
where the sequence of the elements does matter.

Now to conclude with, we can have three kinds of sudoku solutions.
1. Only the first pattern
2. Only the second pattern (see the special case)
3. A mix of the first and the second pattern
Knowing that these patterns must be present greatly helps
solving even the super hard sudokus from Brainbashers.com



